アイマスを愛するプロデューサーの皆様および統計沼に沈まれている皆様。
紅木弘です。
今回はシンデレラガール総選挙について,私が以前から挑戦してみたいと思っていたことをその面白さと価値,難しさも合わせてお話しいたします。
このため,得られました結論についてはまだまだ検討の余地があるものとしてお考えください。
そんな中途半端な話をするなと言われてしまいそうですが,おそらく今年も行われるであろう第10回総選挙に向けまして,私なりの選挙活動の一環としてお話しさせていただきます。
むしろ,この問題に対してどうすれば解決できるのか。たくさんの方からのご意見をちょうだいしたく思っております。
以上のことをご留意いただき,以下で本題に移らせていただきます。
- 総票数を予想できるようになればできること
- 対数正規分布に基づく総選挙総評数推定
- アクティブ数からの総票数推定と実際の獲得票の比較
- 対数正規分布による推定の限界
- 追記:第10回シンデレラガール総選挙Top 10予想得票数
- まとめ
総票数を予想できるようになればできること
以前の記事において,シンデレラガール総選挙でシンデレラガール(順位が1位)となっているアイドルは,総票数の3.5%程度を獲得している。という考察を行いました。
同時に,2位が毎回2.5%程度を獲得しているという傾向から,シンデレラガール総選挙でシンデレラガールになるためには,総票数の3.0%を獲得すればよい。という結論を得ました。
この傾向は第5回総選挙から変わらず,ボイスアイドルオーディションの同時開催や課金票の大幅な増加というレギュレーションに大きな変更があった前回の総選挙である第9回総選挙でも同じ傾向にあったことから,次回総選挙以降でもこの傾向は変わらないものと予想しております。
上記考察に関する記事です。よろしければ,こちらもご覧ください。
idolmaster-statistics.hatenablog.com
idolmaster-statistics.hatenablog.com
これは言い換えれば,総票数が予想できればシンデレラガールになるために必要な票数を推定できることを意味します。
票数が推定できれば,例えば「○○票を集めて△△をシンデレラガールにしよう!」といった総選挙プロモーションが可能となります。同様に「××票を集めて□□を50位圏内に入れよう!」といった総選挙プロモーションも可能です。
すなわち,総選挙プロモーションをより具体的に行うことが可能となるのです。
私見ではありますが,これが実現できる意味は大きいと考えます。なぜなら,自分が投票した票が総選挙の順位にどう影響したのかをより具体的に,達成感を持った上で実感することができるようになるからです。
よって,私は第10回総選挙において,順位の予想ももちろんですが,この総票数とTop10の獲得票数の予想を行いたいと思っております。
ただし,これを実現するためには前提として,総選挙期間中に総票数をどうやって予想するのかという大問題があります。
本記事ではこの問題を解決する方法として,イベントを利用したアクティブユーザー数と1アカウントが入手可能な票数から,対数正規分布に基づき予想する方法を用います。また,この限界についても述べます。
対数正規分布に基づく総選挙総評数推定
推定方法~第5回総選挙を例に~
対数正規分布とは,統計に用いる分布の1つであり,所得や資産の分布として当てはまることが多いとされている分布です。
シンデレラガール総選挙においても,ある票数をピークとして,投票できる票数が多ければ多いほど,その票数を持っている人は少なくなる傾向にあるはずなので,対数正規分布上にユーザーが分布していると仮定します。
すなわち,1アカウントが入手可能な票数を入手した上で,所持している票数に対する人数の変化が対数正規分布に従うと仮定すれば,アクティブユーザー数との比較を行うことによって,総票数を推定できるということです。
言葉だけではわかりにくいと思いますので,第5回総選挙を例に実際にやってみます。
第5回総選挙において,ログインやイベントへの参加によって入手できる票(以下,無課金票)は517票。ガチャを回す際に入手できる票(以下,課金票)は1629票。合計2146票が1アカウントが投票可能な最大票数です。
また,イベント期間中に1ptでもポイントを取得したユーザーの数をアクティブユーザー数とすると,第5回総選挙期間中に開催されたイベントにおけるアクティブユーザー数の平均は94724人でした。
さらに,以前の考察より,第5回総選挙における総票数は29085818票であると推定されております。
これを踏まえた上で,以下の条件となるように対数正規分布のパラメータである平均と標準偏差を設定します。
- 変数 x = (投票数) / 500 として対数正規分布を入手する。
- 最大票数に最低でも1人が存在する。
- 最大無課金票に対して10%毎の割合をピークとする。
- 対数正規分布から入手した総人数とイベントにより入手したアクティブユーザー数の誤差が最小。
これらの条件を満たしたときの対数正規分布を図1に示します。また,このときの各パラメータとアクティブユーザー数および総票数との誤差を表1に示します。


なお,上記図と表において,ピークが80%以上では上記の条件を満たすパラメータを設定できませんでした。
これらの結果より,第5回総選挙では無課金票を全体の20%を獲得したユーザーが最も多い場合の対数正規分布が総選挙結果に基づく推定総票数との総票数差が小さいことがわかりました。
これと同様の推定を第7回から第9回までの総選挙で行います。
ただし,第7回総選挙からはデレステと同時開催となったため,総票数の誤差率についてはモバマスとデレステの合計票数との比較とします。また,第7回および第8回のデレステにおける対数正規分布を獲得する場合の変数 x は,無課金がと課金票の関係から x = (投票数) / 200 とします。
なお,第6回総選挙については課金票についての調査できなかったため,省略しております(情報提供求めます!)。
第7回総選挙
第7回総選挙において,モバマスの各値は以下のようでした。
無課金票:514票
課金票:1148票
1アカウントが投票可能な最大票数:1662票
アクティブユーザー数:75388人
同様にデレステの各値は以下のようでした。
無課金票:95票
課金票:500票
1アカウントが投票可能な最大票数:595票
アクティブユーザー数:370627人
また,第7回総選挙の推定総票数は70839930票です。
以上を踏まえ,表2にモバマスおよびデレステの対数正規分布の各パラメータとアクティブユーザー数との誤差を示します。また,表3に表2に基づく総票数との誤差率を示し,図2に総票数との誤差率最小のときの対数正規分布を示します。



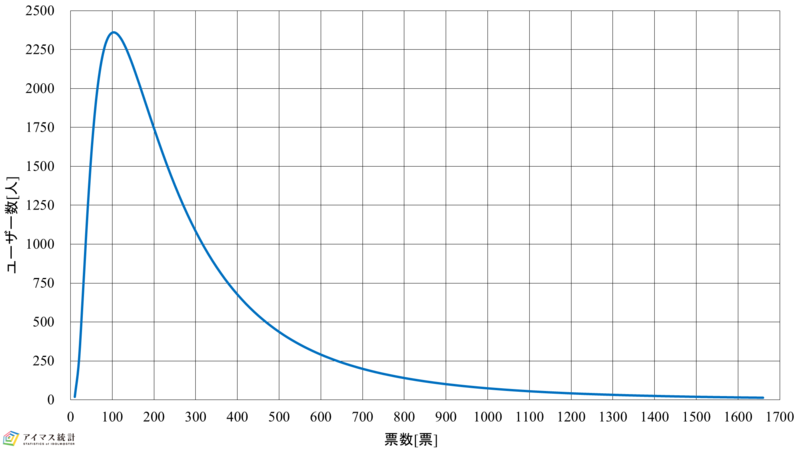
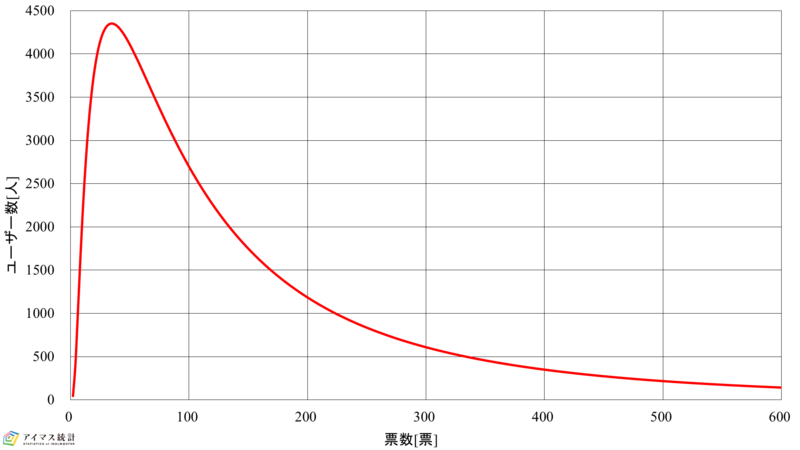
図2-1 第7回総選挙対数正規分布(モバマス) 図2-2 第7回総選挙対数正規分布(モバマス)
これらの結果より,モバマスおよびデレステもアクティブユーザー数についてはピークの値が大きい,つまり,無課金票をより多く獲得したアカウントが多いほど誤差率は小さくなりますが,総票数の点で見てみると,モバマスが20%,デレステが30%をピークとしたものの誤差率が最小となることがわかります。
そもそもとして,ユーザーの多くが無課金票全てを獲得しているという仮定はあまりに現実的でないため,この結果は妥当であると考えます。
第8回総選挙
第8回総選挙において,モバマスの各値は以下のようでした。
無課金票:902票
課金票:1257票
1アカウントが投票可能な最大票数:2159票
アクティブユーザー数:66966人
同様にデレステの各値は以下のようでした。
無課金票:122票
課金票:1000票
1アカウントが投票可能な最大票数:1122票
アクティブユーザー数:329112人
また,第8回総選挙の推定総票数は87963110票です。
以上を踏まえ,表4にモバマスおよびデレステの対数正規分布の各パラメータとアクティブユーザー数との誤差を示します。また,表5に表4に基づく総票数との誤差率を示し,図3に総票数との誤差率最小のときの対数正規分布を示します。




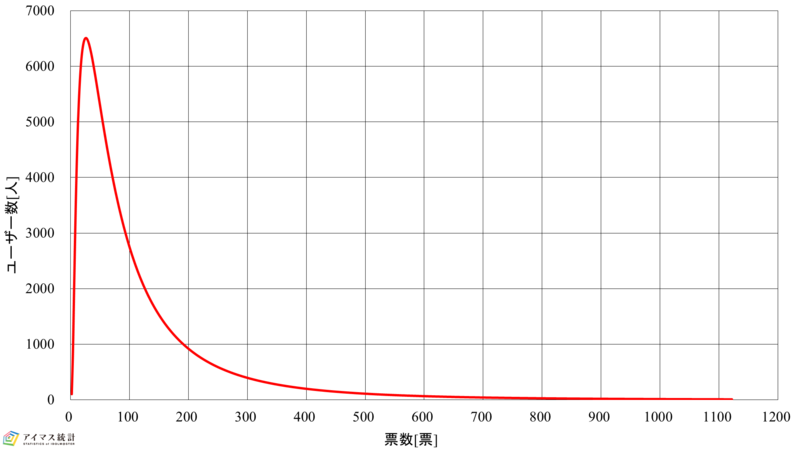
図3-1 第7回総選挙対数正規分布(モバマス) 図3-2 第7回総選挙対数正規分布(モバマス)
これらの結果より,モバマスは30%がピーク,デレステは70%がピークの時,総票数の誤差率が最小となることがわかります。次点の場合はモバマスは40%がピーク,デレステは20%がピークの時であり,その差は0.17ポイントです。
この事実から,以下の2つの仮説を立てました。
仮説1はピークがズレるほど課金するユーザーが増加したとは考えにくいため,仮説2が妥当であると考えております。
第9回総選挙
第9回総選挙において,モバマスの各値は以下のようでした。
無課金票:903票
課金票:30000票
1アカウントが投票可能な最大票数:30903票
アクティブユーザー数:52526人
同様にデレステの各値は以下のようでした。
無課金票:888票
課金票:30000票
1アカウントが投票可能な最大票数:30888票
アクティブユーザー数:287031人
また,第9回総選挙の推定総票数は460349467票です。
以上を踏まえ,表6にモバマスおよびデレステの対数正規分布の各パラメータとアクティブユーザー数との誤差を示します。また,表7に表6に基づく総票数との誤差率を示し,図4に総票数との誤差率最小のときの対数正規分布を示します。



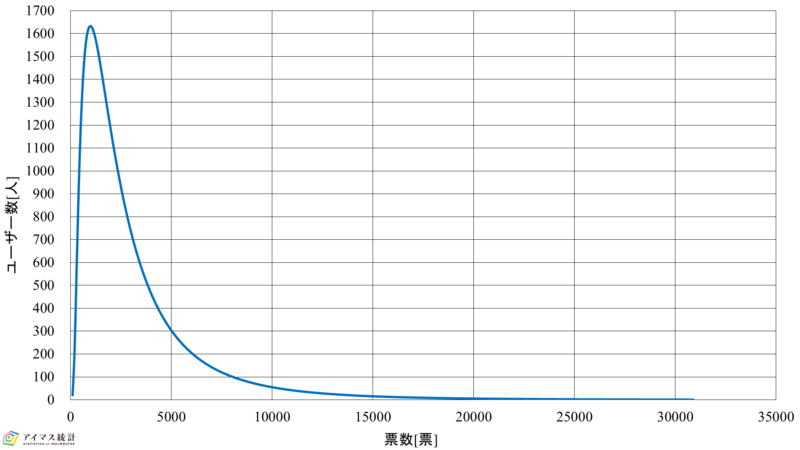
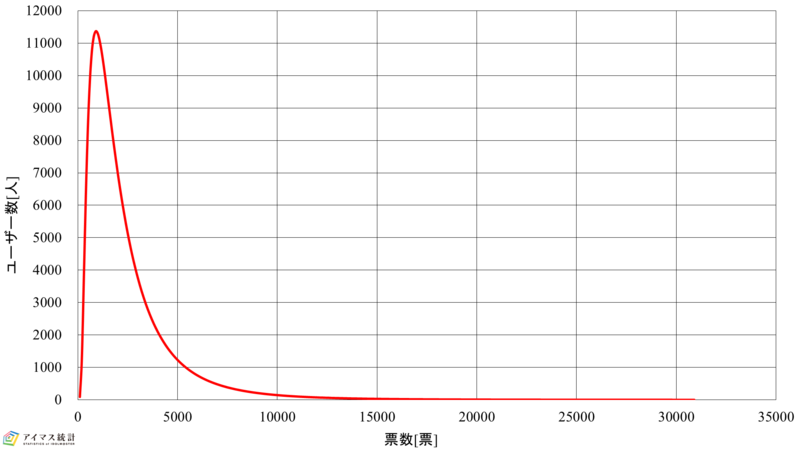
図4-1 第7回総選挙対数正規分布(モバマス) 図4-2 第7回総選挙対数正規分布(モバマス)
これらの結果よりモバマスは30%がピーク,デレステは10%がピークの時,総票数の誤差率が最小となることがわかります。次点の場合はモバマスは20%がピーク,デレステは10%がピークの時であり,その差は0.87ポイントです。
この傾向は第9回総選挙とほぼ同様の結果と言えます。
アクティブ数からの総票数推定と実際の獲得票の比較
さて,ここまでの検討より,アクティブ数から総票数の推定は可能であり,この値と最終結果の順位に基づく総票数との誤差はピーク値さえ正しく設定できれば±5%程度で納めることができることがわかりました。
ここで,本記事の本題である,シンデレラガールに必要な票数の推定に移ります。
前述の通り,シンデレラガール総選挙でシンデレラガールになるアイドルは総票数の3.5%程度を獲得しており,この傾向が今後も続くと仮定します。
このとき,総票数の誤差が推定シンデレラガール獲得票数に与える影響を第9回総選挙を例に表8に示します。
なお,第9回総選挙でシンデレラガールとなった北条加蓮の獲得票数は16926974票であり,総得票数の約3.7%を獲得したと推定しております。

同表より,総票数の誤差が±5%であれば,シンデレラガール獲得票数は±10%以内に,±10%であれば±15%以内に納めることが可能であることがわかります。
また,他の総選挙の結果においても同様の結果を得ました。
すなわち,これまでの考察より,ピーク値さえ正しく設定できれば,シンデレラガール総選挙の総票数は±5%以内で事前推定可能であり,さらに,シンデレラガールの獲得票数も±10%以内で事前推定が可能となることがわかりました。
ただし,総票数が増えれば当然この5%,10%の値が大きくなるため,この点は忘れてはなりません。
対数正規分布による推定の限界
この推定は前提として,シンデレラガール総選挙は所持している票数に対する人数の変化が対数正規分布に従うという仮定に立っております。
したがって,この仮定が成り立たない場合は推定精度が低下します。
例えば,第9回総選挙では総選挙応援セットとして課金票を300枚50セットを2回に分けて販売しました。
このような場合において,1セットや10セット,50セットといったキリのよい購入をしたアカウントがピークとして立つ可能性は十分に考えられます。もっと言えば,50セット購入したアカウント数は49セット購入したアカウントよりも数が多いと直感的には考えられます。したがって,この時点で対数正規分布に従うという仮定については疑問を呈さざるおえません。
一方で,どのくらいのユーザーが課金票を購入し,何セット購入したアカウントがどのくらいあるかを推定することは現状不可能です。
また,課金票の購入期限は総選挙終了当日までであるため,駆け込み購入をする方も当然存在する以上,これを踏まえたリアルタイム推定は困難を極めます。
加えて,本記事の目的は総選挙開始の早い段階でシンデレラガールになるために必要な票数を推定することにあるため,そもそもとしてリアルタイム性が存在するような推定は目的から外れます。
よって本記事の考察は,対数正規分布に従うという仮定が成り立たない可能性がある上で,これに従った場合における推定であり,推定には限界がある点はご留意ください。
追記:第10回シンデレラガール総選挙Top 10予想得票数
2021/4/19 15:00時点
アクティブユーザー数
前回のイベントより,
モバマス:32584
デレステ:211010
1アカウントが獲得できる票数
モバ・デレ共に
無課金:900票
課金:30000票。
と仮定。
上記データに基づき,推定総得票数を約3億2千万票と推定。
#第10回シンデレラガール総選挙#アイマス統計
— 紅木 弘@統計屋(自称) (@hiroshiakagi398) 2021年4月20日
【2021/4/19 15:00時点】
第10回シンデレラガール総選挙において,1位(シンデレラガール)は約1121万3000票獲得すると推定します。
2位以下は表の通りです。
あくまで過去の総選挙傾向からの推定です。ご留意ください。 pic.twitter.com/JM1p3n9RDp

2021/4/28 12:00時点
アクティブユーザー数
前回のイベントより,
モバマス:42541
デレステ:217784
1アカウントが獲得できる票数
モバ・デレ共に
無課金:900票
課金:30000票。
と仮定。
上記データに基づき,推定総得票数を約3億5千万票と推定。
【2021/4/28 12:00時点】
— 紅木 弘@統計屋(自称) (@hiroshiakagi398) 2021年4月28日
第10回シンデレラガール総選挙において,1位(シンデレラガール)は約1219万8000票獲得すると推定しました。
2位以下は表の通りです。
あくまで過去の総選挙傾向からの推定です。ご留意ください。#第10回シンデレラガール総選挙#アイマス統計 pic.twitter.com/4Vgb5Xyihz

2021/5/4 18:00時点
アクティブユーザー数
前回のイベントより,
モバマス:38415
デレステ:217784
1アカウントが獲得できる票数
モバ・デレ共に
無課金:900票
課金:30000票。
と仮定。
上記データに基づき,推定総得票数を約3億4千万票と推定。
#第10回シンデレラガール総選挙#アイマス統計
— 紅木 弘@統計屋(自称) (@hiroshiakagi398) 2021年5月4日
【2021/5/4 18:00時点】
第10回シンデレラガール総選挙において,1位(シンデレラガール)は約1190万8000票獲得すると推定しました。
2位以下は表の通りです。
以下,推定の根拠を示します。 pic.twitter.com/uJhvOGHhPR

2021/5/8 20:00時点
アクティブユーザー数
前回のイベントより,
モバマス:38415
デレステ:204133
1アカウントが獲得できる票数
モバ・デレ共に
無課金:900票
課金:30000票。
と仮定。
上記データに基づき,推定総得票数を約3億2千万票と推定。
#第10回シンデレラガール総選挙#アイマス統計
— 紅木 弘@統計屋(自称) (@hiroshiakagi398) 2021年5月8日
【2021/5/8 20:00時点】
第10回シンデレラガール総選挙において,1位(シンデレラガール)は約1133万票獲得すると推定しました。
2位以下は表の通りです。
以下,推定の根拠を示します。 pic.twitter.com/vRGhVH427S

2021/5/12 18:00時点
アクティブユーザー数
直近のイベントより
モバマス:37776
デレステ:204133
と仮定。
1アカウントが獲得できる
無課金票
モバマス:882票
デレステ:882票
課金票
モバデレ共に30000票
なお,票数についてはこれで確定。
上記仮定に基づき,推定総票数を約3億2千2百万票と推定。
#第10回シンデレラガール総選挙#アイマス統計
— 紅木 弘@統計屋(自称) (@hiroshiakagi398) 2021年5月12日
【2021/5/12 18:00時点】
第10回シンデレラガール総選挙において,1位(シンデレラガール)は約1130万票獲得すると推定しました。
2位以下は表の通りです。
以下,推定の根拠を示します。 pic.twitter.com/NEgHxf1RcA

まとめ
以上,まとめに入ります。
過去の検討から,総票数が予想できればシンデレラガールになるために必要な票数を推定できるという前提に立ち,シンデレラガール総選挙は所持している票数に対する人数の変化が対数正規分布に従うという仮定をした場合において,その推定精度はどのくらいになるかの検討を行いました。
この結果,対数正規分布のピークの値を正しく設定できれば±5%程度の精度で総票数を推定できることを確認しました。また,このピークについてですが,獲得可能な無課金票の20%~40%の範囲であり,過去の総選挙における考察から,モバマスは30%~40%,デレステは10%~20%にあることを確認しました。
また,上記推定総票数からシンデレラガールになるための必要獲得総票数と実際の獲得数の比較を行った結果,総票数を±5%程度に納めることができれば,誤差±10%の精度で獲得票数を推定可能であることを確認しました。
なお,対数正規分布に従うという仮定が成り立たない可能性についても言及しましたが,これについては本記事の目的からはやむを得ないことであり,この仮定が成り立たない場合の推定については今後の課題とさせていただきます。
第10回総選挙では早い段階で総票数とシンデレラガールの獲得票数の推定を公表する予定ですので,これが当たっているかどうかについても楽しみにしていただけますと幸いです。
それでは,これにて本記事を締めさせていただきます。
統計の力で,アイマスがもっと好きになる。
紅木弘がお送りしました。
